1. 깊이 우선 탐색이란
- 맹목적 탐색 방법 중 하나로 연결된 노드(자식노드)를 따라서 계속 방문한 후 연결된 노드가 없을 경우, 이전 노드로 되돌아 다른 연결된 노드를 탐색하는 방
- 노드들의 자식들을 먼저 탐색하는 방식으로 스택을 활용한다.
- 스택을 사용하지 않고 재귀함수를 사용해서도 구현이 가능하다.
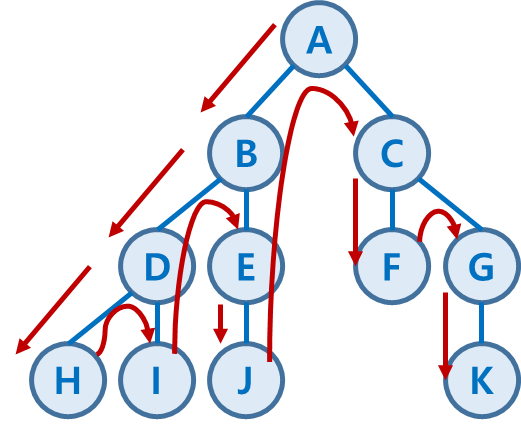
1) DFS의 흐름
- 스택에 시작노드를 담고 방문처리한다.
- 스택의 최상단을 확인한다.
- 최상단 노드와 연결된 노드 중 방문하지 않은 노드가 있으면 스택에 담고 방문 처리한다.
- 방문하지 않은 연결된 노드가 없으면 스택에서 제거한다.
- 2~4를 반복한다.
2. DFS 구현해보기
import java.util.*;
public class DFSEx {
public static void main(String[] args) {
HashMap<String, ArrayList<String>> graph = new HashMap<>();
graph.put("A", new ArrayList<String>(Arrays.asList("B", "C")));
graph.put("B", new ArrayList<String>(Arrays.asList("A", "D", "E")));
graph.put("C", new ArrayList<String>(Arrays.asList("A", "F", "G")));
graph.put("D", new ArrayList<String>(Arrays.asList("B", "H", "I")));
graph.put("E", new ArrayList<String>(Arrays.asList("J")));
graph.put("F", new ArrayList<String>(Arrays.asList("C")));
graph.put("G", new ArrayList<String>(Arrays.asList("C", "K")));
graph.put("H", new ArrayList<String>(Arrays.asList("D")));
graph.put("I", new ArrayList<String>(Arrays.asList("D")));
graph.put("J", new ArrayList<String>(Arrays.asList("E")));
graph.put("K", new ArrayList<String>(Arrays.asList("G")));
ArrayList<String> result = dfs(graph, "A");
System.out.println(result);
}
public static ArrayList<String> dfs(HashMap<String, ArrayList<String>> graph, String startNode) {
ArrayList<String> visited = new ArrayList<>(); // 큐
ArrayList<String> notVisitedYet = new ArrayList<>(); // 스택
notVisitedYet.add(startNode);
while (!notVisitedYet.isEmpty()) {
String node = notVisitedYet.remove(notVisitedYet.size() - 1);
if (!visited.contains(node)) {
visited.add(node);
notVisitedYet.addAll(graph.get(node));
}
}
return visited;
}
}- 스택을 이용해서 구현하기
import java.util.Stack;
public class DFSEx {
public static void main(String[] args) {
int[][] graph = {{}, {2, 3, 8}, {1, 6}, {1, 4}, {3, 5, 7}, {4}, {2}, {4}, {1, 9, 10}, {8}, {8}};
// int[][] graph = {{}, {2, 3, 8}, {1, 6, 8}, {1, 5}, {5, 7}, {3, 4, 7}, {2}, {4, 5}, {1, 2}};
String result = dfs(graph, 1);
System.out.println(result);
}
public static String dfs(int[][] graph, int startNode) {
Stack<Integer> notVisitedYet = new Stack<>();
boolean[] visited = new boolean[graph.length];
StringBuilder sb = new StringBuilder();
notVisitedYet.push(startNode);
visited[startNode] = true;
sb.append("[ ");
while (!notVisitedYet.isEmpty()) {
Integer nodeIdx = notVisitedYet.pop();
sb.append(nodeIdx + " ");
for (int i = 0; i < graph[nodeIdx].length; i++) {
int linkedNode = graph[nodeIdx][i];
if (!visited[linkedNode]) {
notVisitedYet.push(linkedNode);
visited[linkedNode] = true;
}
}
}
sb.append("]");
return sb.toString();
}
}- 재귀함수를 사용해서 구현하기
import java.util.Stack;
public class DFSEx {
public static void main(String[] args) {
int[][] graph = {{}, {2, 3, 8}, {1, 6}, {1, 4}, {3, 5, 7}, {4}, {2}, {4}, {1, 9, 10}, {8}, {8}};
// int[][] graph = {{}, {2, 3, 8}, {1, 6, 8}, {1, 5}, {5, 7}, {3, 4, 7}, {2}, {4, 5}, {1, 2}};
boolean[] visited = new boolean[graph.length];
dfs(graph, visited, 1);
}
private static void dfs(int[][] graph, boolean[] visited, int startNode) {
visited[startNode] = true;
System.out.print(startNode + " ");
for (int node : graph[startNode]) {
if (!visited[node]) {
dfs2(graph, visited, node);
}
}
}
}참고 : BFS
너비 우선 탐색(BFS : Breadth First Search)
1. 너비 우선 탐색이란 맹목적 탐색 방법 중의 하나로 시작 정점을 방문한 후, 한 노드와 같은 레벨에 있는 노드들을 먼저 탐색하는 방법으로 큐나 연결리스트를 활용한다. 인접한 모든 정점들을
hyunbenny.tistory.com
'algorithm' 카테고리의 다른 글
| [알고리즘] 탐욕법(Greedy) (0) | 2023.02.05 |
|---|---|
| [알고리즘] 구간 합 (0) | 2023.02.03 |
| [알고리즘] 너비 우선 탐색(BFS : Breadth First Search) (0) | 2023.01.31 |
| [알고리즘] 분할정복(Divide and Conquer) (0) | 2023.01.30 |
| [알고리즘] 순차탐색과 이진탐색 (0) | 2023.01.30 |
